Reviving Fibonacci Hashing: An Innovative Approach to Data Mapping in Computer Science
In the ever-evolving landscape of computer science, few concepts are as ubiquitous and essential as hashing and hash functions. These mathematical techniques play a crucial role in various domains, including data security, encryption, password management, and cryptocurrency. At their core, hashing allows for the efficient mapping of large or complex data sets to a smaller, fixed-size representation, significantly enhancing data retrieval speed for computers.
Recently, a researcher named Malte has delved into the intricacies of hash functions and unearthed a method known as Fibonacci hashing. This intriguing technique appears to have been largely overlooked in modern computing yet offers the potential to accelerate data lookup processes even further than traditional methods.
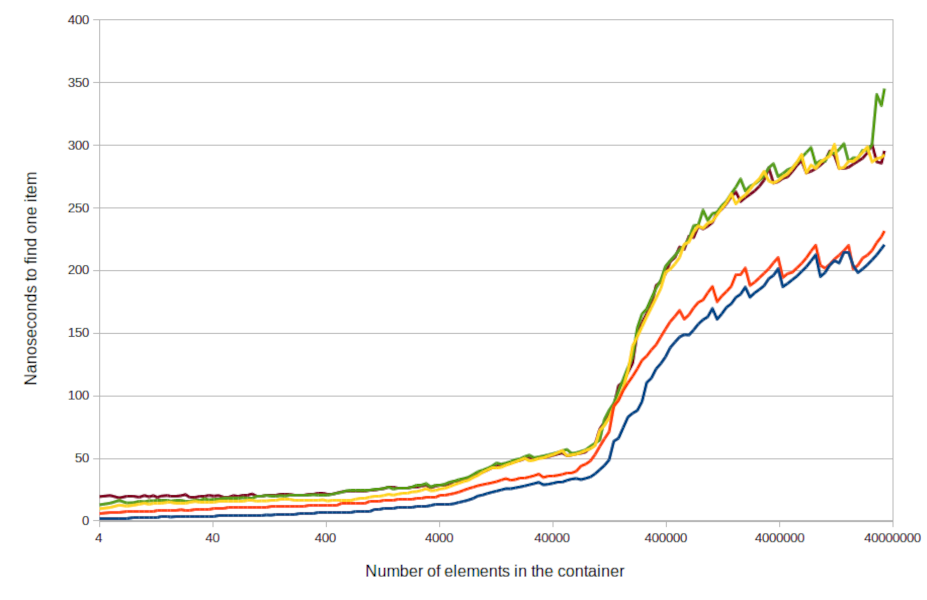
In standard hashing operations, raw data is transformed into a new representation, with a portion of this transformed value employed to determine a specific storage location. Typically, this determination is achieved using an integer modulo function. However, a common challenge in hashing arises when two distinct pieces of data yield the same value post-modulo operation. This phenomenon, known as a collision, leads to both pieces of data being stored at the same location, which can hamper data retrieval efficiency.
Fibonacci hashing presents a sophisticated alternative. Instead of relying on the modulo function, this method uses the golden ratio to dictate the final storage location of the data. This approach significantly reduces the incidence of collisions and enhances speed, allowing for a more efficient distribution of values across the fixed-size set. Fibonacci hashing also ensures that the smaller fixed-size set is utilized more evenly, provided the input data does not contain a large number of Fibonacci numbers itself.
In exploring the mathematics underpinning Fibonacci hashing, Malte's findings suggest that this approach outperforms traditional integer modulo methods concerning the mapping aspect of hash functions. Some commentators have noted that Fibonacci hashing can be classified as a specific instance of a broader category known as multiplicative hashing. For developers and engineers employing hash functions in their coding practices, Malte's work is certainly worth investigating. Although he acknowledges his own limitations in this branch of computer science, he provides an in-depth analysis of Fibonacci hashing that merits attention.
For those who are new to the topic of hashing, consider the implications of reverse-hashing, which is notoriously challenging. A notable case illustrating this difficulty involved an individual who offered a substantial bounty for the recovery of a bitcoin wallet, highlighting the complex nature of hashing and its security applications.